My answer is:
dcAdt=−2k1⋅(cA)2⋅(cB)
dcBdt=−k1⋅(cA)2⋅(cB)
dcCdt=−3k1⋅(cA)2⋅(cB)
I could be wrong.
As promised, I will attempt an abstraction. aA+bB+cC
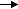
dD+eE+fF (I may not write all 6 ODEs), order is x wrt A, y wrt B, z wrt C.
dcAdt=−ak1⋅(cA)x⋅(cB)y⋅(cC)zdcBdt=−bk1⋅(cA)x⋅(cB)y⋅(cC)zdcCdt=−ck1⋅(cA)x⋅(cB)y⋅(cC)zdcDdt=dk1⋅(cA)x⋅(cB)y⋅(cC)zdcEdt=ek1⋅(cA)x⋅(cB)y⋅(cC)zThe important thing to note is:
dcSpeciesdt=vSpecies⋅k1⋅(cA)x⋅(cB)y⋅(cC)zWhere v
Species is the stoichiometric coefficient on that species in the reaction, multiplied by -1 if the species is a reactant and +1 if the species is a product.
The equations apply regardless of the values of x,y,z, including when they equal 0?