Alright, building an MO diagram is a fine place to start, but may be a little overkill. I think you have most of the pieces there to do it, but we can simplify things. We don't need to get into hybridization and all that stuff for this problem. All we want to know are the orbitals involved, and what the symmetry of those orbitals are in the C
2v point group - and only those involved with the carbonyl group.
Considering just the C and the O, there are basically five molecular orbitals to worry about:
1. A σ orbital between C and O.
2. A π orbital between C and O.
3. Two non-bonding atomic orbitals (
n) on oxygen
4. A π* orbital between C and O.
5. A σ* orbital between C and O.
I've already ordered these from low to high energy. This is all in line with what you wrote in your last post, more or less. The nonbonding orbitals are intemediate in energy between the π and π* orbitals. This should be intuitive, since the π and π* orbitals are stabilized and destabilized, respectively, compared to nonbonding
p-orbitals, even if one is carbon and the other oxygen. So, your HOMO is going to be one of the nonbonding orbitals on oxygen and the LUMO is going to be the π* orbital. The lowest energy transition for carbonyl is π*
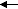 n
n. Note that you have higher energy transitions (e.g., between the π and π* orbitals), and it wouldn't be a bad idea to go through the exercise of showing whether these transitions are symmetry allowed or forbidden.
On to step 2: assign symmetry labels to the participating states. The participating orbitals have been defined, but not the states. We can go whole hog here but again some simplification is in order. Any filled orbital has complete symmetry (A
1), because any symmetry designation times itself is completely symmetric, so electrons in the low lying π and σ orbitals don't really contribute to the state symmetry. So we can just think about what happens to the electrons in the nonbonding and π* orbitals. If our transition is π*
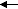 n
n, then the states we have to worry about are
n1π*1 and n2. Can we determine what symmetry representations these states conform to?
To get you started, call the axis of the molecule the z-axis and the zy plane contains the R groups. In this scheme, using C
2v symmetry group, assign a representation for each of the molecular orbitals defined above. Then, it is straightforward to assign the symmetry labels to the participating states simply by doing a little multiplication of the orbital representations. If you need some help with that, let me know. Once you have symmetry designations for the states, we can look at why the transition is forbidden.
One other thing, the two nonbonding orbitals typically transform together. For simplicity, I think it is easier just to visualize the participating nonbonding electrons to be located in a straight-up (i.e. unhybridized)
py orbital. Use this to determine the symmetry of the nonbonding electrons. It's not strictly correct but the symmetry designation will be.
NB: The π (pi) symbol and letter n symbol look practically identical on this forum! I've tried to help that out by italicizing the "n" where possible.