It means the molecular orbitals are mixing character, which can happen if they have mutually appropriate symmetry. The degree of mixing depends on spatial overlap as well as relative energy.
A classical analogy is if you bring two bar magnets close together. Each magnet in isolation has a certain amount of reference energy. Now when you bring them together, the new potential energy will depend on their mutual orientation. First, suppose you bring them together in perpendicular orientation, with either head of one approaching the middle of the other, to form a "T" shape. Here the symmetries of the two are not compatible, and what you get is no interaction at all. They neither repel or attract. The potential energy of the system doesn't change.
Now, suppose you bring them in parallel to each other, like this:


or
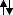
(the arrow indicates the direction of the magnetic moment). There are two possible ways you can bring them together, as indicated. One is that they are head to head (parallel,


) and the other is that they are head to tail (antiparallel,
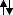
). In both cases the symmetry is appropriate for interaction, but the type of interaction is different. In a head to tail orientation, there is an attractive force, which lowers the potential energy of the system relative to the potential energy of two isolated magnets (you'd have to supply work to separate them), and the degree of energy lowering depends on the starting strength of the magnets and how close you bring them together. In a head to head orientation, the magnets repel each other and the potential energy is raised compared to the potential energy of two isolated magnets. The degree of repulsion when antiparallel is ~ equal to the degree of attraction in the opposite, parallel case.
A final case is if you bring the two magnets together so that they are laying in a single line, like this:


or

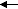
. Again the symmetry is appropriate for mixing, and we have the same possibilities as before: a head to head and a head to tail. And as before a head to tail results in a lowering of the potential energy (they stick together) and a raising of the potential energy (they force apart), respectively. The only real difference between


/
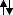
and


/

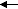
is the magnitude of interaction: the potential energy changes of


/

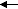
are actually greater (twice larger, in the point dipole approximation), because the parts of similar polarity are farther from each other (or twice closer, for the unfavorable

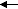
interaction) than if they are


/
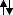
.
This may seem rather abstract but it's actually fairly relevant to orbital interaction, which is governed in large part by the interaction of the magnetic fields created by moving electrons. In fact, p-orbitals interact in a very similar way to classical magnetic dipoles, the difference being that energies and other observables are quantized. Energies of interaction can take on only certain values and this restricts where electrons in those orbitals can be found in space. Two p-orbitals interacting in a


orientation would be a sigma bond interaction between two adjacent p-orbitals and the

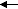
would be a sigma antibonding interaction between two adjacent p-orbitals, with corresponding lowering and raising of the interaction (bond/antibond) energy compared to isolated p-orbitals. You probably can guess that the


and


interactions correspond to pi-bonding and pi-antibonding interactions, respectively. And yes, as the simple classical point dipole interaction suggests, pi-bonds are weaker than sigma bonds because the


-type interactions are generally weaker than

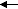
-type interactions. In QM formulation we speak of Coulomb, exchange and overlap integrals, but it is effectively the same thing with the same general result. Finally, if you tried to bring together two p-orbitals in a head to waist orientation


, there is no bonding interaction at all because of the way the fields cancel each other out. The symmetry isn't right.
Also note here that the dependence of the "pushing" effect, as you call it, on the relative starting energies of the isolated orbitals is analogous to combining classical magnets of different strengths. If you take a really strong bar magnet and put it next to a really little bar magnet, the same types of interactions will occur, but the relative interaction energy will be smaller. (A weak magnet isn't going to perturb the energy of the strong magnetic as much as another strong magnet would). This is why 1s orbitals don't interact much with 4s orbitals, for example, even though they have the appropriate symmetry to do so (proximity of the orbitals is also a factor here as well, to be fair).
Interactions between d-orbitals and s-orbitals work essentially the same way as everything described above, but now your symmetry combinations are different and cannot be compared so neatly to the classical analogy of a bar magnet.

Note that this analogy also applies to other molecular orbital interactions such a J- and H-aggregates, excitons in conducting polymers, and so on.