Hi
What are the Gibbs free Energy of a system containing multiple species in both gas and liquid phase?
The specific system I'm trying to solve by minimizing the Gibbs free Energy are:
SO
2(g) 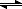
SO
2(aq)SO
2(aq) + H
2O
(l) 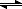
HSO
-3(aq) + H
+(aq)CO
2(g) 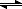
CO
2(aq)CO
2(aq) + H
2O
(l) 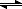
HCO
-3(aq) + H
+(aq)I don't want to solve it using Henry's Law & Equilibrium constants because I want to add constraints on some of the variables later on.
My best guess are the below function but I'm not sure if it's correct. (The pressure are assumed constant at 1atm)
[tex] \Delta T = T - 298.15 [/tex]
[tex] n_{gas} = n_{SO_{2(g)}} + n_{CO_{2(g)}} [/tex] [tex] n_{liq} = n_{SO_{2(aq)}} + n_{HSO^-_{3(aq)}} + n_{CO_{2(aq)}} + n_{HCO^-_{3(aq)}} + n_{H_2O_{(l)}} + n_{H^+_{(aq)}} [/tex]
[tex] \mu_{SO_{2(g)}} = G_{f,SO_{2(g)}}^0 - S^0_{SO_{2(g)}} \Delta T + RT \ln \left\{ \frac{n_{SO_{2(g)}}}{n_{gas}} \right\} [/tex] [tex] \mu_{CO_{2(g)}} = G_{f,CO_{2(g)}}^0 - S^0_{CO_{2(g)}} \Delta T + RT \ln \left\{ \frac{n_{CO_{2(g)}}}{n_{gas}} \right\} [/tex] [tex] \mu_{HSO^-_{3(aq)}} = G_{f,HSO^-_{3(aq)}}^0 - S^0_{HSO^-_{3(aq)}} \Delta T + RT \ln \left\{ \frac{n_{HSO^-_{3(aq)}}}{n_{liq}} \right\} [/tex] etc...
[tex] G = \mu_{SO_{2(g)}} n_{SO_{2(g)}} + \mu_{CO_{2(g)}} n_{CO_{2(g)}} + \mu_{HSO^-_{3(aq)}} n_{HSO^-_{3(aq)}} + \mu_{HCO^-_{3(aq)}} n_{HCO^-_{3(aq)}} + \mu_{H^+_{(aq)}} n_{H^+_{(aq)}} + \mu_{H_2O{(l)}} n_{H_2O{(l)}} [/tex]