I end up with 4!!!!!
3N-5 = Ag + B1u +B2u + B3u
All good. Just a few notes here for your benefit:
(1) The reason we don't have 3N-6 in the linear case is because there is no rotation around the long axis, so no Rz.
(2) To show you how these symmetry assignments make some physical sense (otherwise, they are just letters and numbers), we can consider the actual vibrational modes for CO
2. Because it is a simple molecule, this is pretty easy. There is a symmetric stretch, an asymmetric stretch, and two mutually perpendicular bending modes.
The symmetric stretch looks like this:
O

C
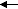
O and O
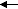
C

O
Can you see how this corresponds to the Ag symmetry class? Perform the symmetry operations for the D2h group and see how the Ag representation fits. No matter what symmetry elements you operate with, the direction of the arrows stays the same. It's all 1's. Ag. Note that the Ag representation does not have a linear (x,y, or z) basis, so we predict that the symmetric stretch is not IR active. This agrees with experiment. The symmetric stretch results in no net change in the molecular dipole moment, which is required for IR activity. Also note that the Ag symmetry representation does have a quadratic basis, which predicts the symmetric stretch should be Raman active. This also agrees with experiment. The symmetric stretch results in a change in the polarizability, which is required for a Raman peak to show. (Don't know if you've learned this; if not, ignore.)
The asymmetric stretch looks like this:
O

C

O and O
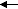
C
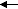
O
This corresponds to the B1u symmetry representation. Can you see why? The symmetry representation is 1 1 -1 -1 -1 -1 1 1. Let's just take two of these as examples. First: the xy mirror plane. If you reflect through this, the arrows change directions, corresponding to a "-1". Second" the xz mirror plane. If you reflect through this, the arrows do NOT change directions, corresponding to a "1". The rest will check out, too - you should look at it and verify that you see this. B1u DOES have a linear basis (z). We predict that the B1u vibrational mode will be IR active. And yes, it turns, out that if you shrink one C=O bond and stretch the other, the dipole moment changes in (surprise!) the z-direction. You will note that the mode is NOT Raman active. This kind of makes sense - if you shrink one C=O bond and stretch the other, the effective volume of the molecular orbitals doesn't really change that much. Polarizability thus doesn't change, thus this mode is forbidden for the Raman spectrum. (Again, don't worry about this if you haven't talked about Raman.)
That leaves B2u and B3u. These are assigned to the two mutually perpendicular bending modes. These will be harder to represent here with arrows, but it looks something like this for the bend along the x direction (where the plane of your screen in the xz plane):



and



where the first, second and third arrows represent the direction of motion for O, C, and O, respectively.
The other one will be identical except the arrows will be coming in and out of the screen, along the yz plane. Both B2u and B3u have a linear bases and are therefore IR active along the y and x directions, respectively. So the one I drew above with arrows is B3u and the one with arrows coming out of the computer screen is B2u. You'll see that the symmetry representations are identical except for the signs corresponding to symmetry operations with only one component in an x or y direction. (That is C2(y) and C2(x) have opposite signs). Try to think about these symmetry operations for these two representations and how they correspond to changes in the directions of the arrows drawn above. This will really help you understand the significance of how group theory representations are assigned to molecular motions during vibrations... and why we use group theory in the first place.
Now one more thing. As your teacher has noted CO
2 does not really belong to the D
2h point group. It belongs to D
∞h. But D2h is easier to use. It's a lower symmetry group, the difference being that we restrict rotation around the z-axis to only a 2-fold rotation, rather than an infinite number of rotations. In practice it doesn't change too much, but we do need to express the vibrational modes in correct symmetry representations. You are lucky here that this is easy because most of your modes have linear bases, so you can simply see where the x,y and z bases are in D
∞h and assign them accordingly. The only one that doesn't, as we've mentioned, is Ag, but finding the corresponding representation in the D
∞h group is straightforward - there's only one totally symmetric representation.
One important distinction - in D
2h, the x and y bases were independent. From a chemical point of view, what this means is that the molecule was assumed to be able to vibrate only along the x or y direction and nothing in between (in a fixed frame). In reality this is not the case. The bending motion can be in any plane that includes the z-axis, and no matter what way the vibration is, the energy is the same. This is why the x,y basis transform together in the D
∞h group as a degenerate pair (with an "E" designation). What this basically translates to is that the first excited bending vibration of CO2 is 2-fold degenerate (two states of identical energy differing only in perpendicular dimensionality), and furthermore that there is no true x- or y- axis, at least from the molecular frame of reference. Note that the other two vibrational modes remain single-dimensional with well defined Cartesian directions.
The linear point groups are strange, so don't worry if you're confused. I'm a little surprised your professor used one for your homework.
Eu+, and the two Pi u should be because they correlate with the B1u, B2u and B3u which is where the x,y,z appears on character chart.
Sound all good?
Almost, B1u (z-basis in D2h) transforms as A1u in D∞h. B2u and B3u transform as the degenerate E1u. Sometimes you'll see this written as Π (and the A's written as Σ, often with +'s and -'s). These are used with term symbols. I'm not sure if you've gotten into that or not. They are handy shorthand (just like the A/B distinction) so you quickly know the parity of the state with respect to specific symmetry operations. This is mostly useful to quickly determine whether certain spectroscopic transitions are allowed or forbidden.
Hope that helps!