That's the curve! Thanks for your reply, the fact is that I don't know much about pH and for some reason fail trying to calculate those points.
Then I used Henderson-Hasselbalch approximation but it fails in the extremes

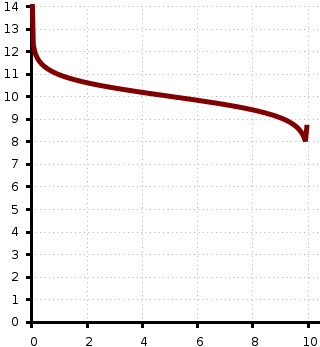
I'm not supposed to make these curves (or calculate pH of any point) but I want to know how and put them in my report.
So I'm possibly wrong but when I have only Na2CO3 I should treat it like a weak base of CO
32- and its kb = 2.1·10
-4. So I solve the quadratic equation:
$$ x^2 + kb\cdot x - kb\cdot concentration = 0 $$
Then to the solution x
1 I obtain pH from:
$$ pH = 14 + log(x_1) $$
And obtain 11.65
I know that if I add some HCl the following reaction takes place:
Na
2CO
3 + HCl

NaHCO
3 + NaCl
And with de NaHCO
3:
CO
32- + H
+ 
HCO3
-Then if I add 10 ml of HCl all the Na
2CO
3 will be replaced by NaHCO
3 and I calculate that pH knowing that HCO3
- kb = 4.8·10
-11 and the concentration is:
$$ Concentration = \frac{0.1\cdot \textit{ml added}}{\textit{total ml}} $$
Then solving again the quadratic equation:
$$ x^2 + kb\cdot x - kb\cdot concentration = 0 $$
And again:
$$ pH = 14 + log(x_1) $$
Obtaining 8.35
For the intermediate points my logic was: take the pH of both, apply exponential to get the [H
+] concentrations, multiply it by their volumen, add the H
+ divide them by the total volume to gent the [H
+] of the solution and apply -log() to get the pH. But that doesn't work.