[Lachln]

TL;DR

• Doing practical report.
• Enthalpy of Combustion (Alcohols).
• Isomers differ in their standard enthalpy of combustion.
• Why?
• Is it something to do with stability? If so, what makes a molecule stable?
• Is it something to do with intermolecular forces?


Hey,

This is my first time asking a question of a forum. Whenever I have trouble seeking answers to my questions online I usually just ask my peers or my teachers. In-case you're wondering, I am currently in Year 11 at an Australia school and, obliviously, one of the subjects I study is Chemistry. 

I have seriously spent countless hours seeking a 'solid' answer to my question. I really hope I will gain some clarity in this forum. I'm actually writing up at prac report.

My first hypothesis for the experiment is "As the carbon chain increases in an alkanol, the heat of combustion will increase." and I completely understand that.

My second hypothesis is, "2.   Straight molecular structures produces a greater heat of combustion whilst a branched molecular structure produces less heat of combustion. As follows, primary alcohols will have greater heat of combustion than secondary or tertiary." My thinking is that hydroxyl (-OH) groups are electron withdrawing so, in alcohols, the more branched the molecule, the less heat of combustion as they are more stable. FEEL FREE TO CORRECT THIS.

To my question: isomers, they have the same molecular weight (almost) and same molecular formula but differ in their structure. If they only differ in their structure, why  do they have different enthalpy of combustions?

I really need a solid explanation. Like I said, I have spent countless hours researching the answer. Is it something to do with the stability of the molecule? (If it has something to do with the stability of the molecule, could you please explain what makes a molecule more/less stable). Is it something to do with the intermolecular forces? I am so lost.

The alcohols I’m experimenting with are: 1-butanol, 2-butanol, Pentane, 1-pentanol, 2-methyl-1-propanol, and 2-methyl-2-propanol.

The amount of time I have dedicated to discovering the answer has astonished me. It's come to the point where paying someone to tell me would actually serve me better.

I'm not giving up on my quest for an answer, ever.

[Corribus]

Making predictions is great. But data doesn't lie.* Let's look at some real combustion data, see what we see.

Combustion data is freely available for many organic compounds at the NIST chemistry webbook.

http://webbook.nist.gov/chemistry/

Let's consider your first question: does the number of carbons in a primary alcohol affect the combustion enthalpy. You predicted that it would increase. Actually, it decreases. (I imagine you meant to say that the absolute magnitude would increase. The combustion enthalpy is negative since the reaction is exothermic.) Here is the data (averaged, because multiple experimental values are provided, values are in kJ/mol):

Alcohol		# of carbons		ΔHc		ΔHc per carbon
Methanol		1		-721		-721
Ethanol		2		-1368		-684
Propanol		3		-2022		-674
Butanol		4		-2670		-668
Pentanol		5		-3328		-666
Hexanol		6		-3981		-663
Octanol		8		-5290		-661
Decanol		10		-6601		-660
Dodecanol		12		-7930		-661
Eicosanol		20		-13130		-656

We must ask ourselves whether this is a really meaningful conclusion, however. After all, these combustion values are in units of energy per mole of alcohol, but a mole of a heavier alcohol produces more products than a mole of a lighter alcohol. Because a reaction enthalpy can be thought of as stoichiometric difference in the energy released when breaking every bond of reactant molecules and the energy consumed when forming every bond of the product molecules, it shouldn't really be surprising that these values become larger for larger molecules. From a practical fuel standpoint, larger molecules have a smaller number of moles per unit volume for an identical concentration, so while burning 1 mole of butanol may release more energy than burning 1 mole of methanol, 1 gram of pure methanol (MW = 32 g/mol) has more moles of fuel than 1 gram of pure butanol (MW = 74 g/mol)... so the effect cancels out. We could easily express those combustion values as heat per gram rather than heat per mole to see the same basis effect as normalizing as "per carbon atom". but per carbon atom is what I'm going to do since it's easier.

A balanced equation for the combustion of a generic linear alcohol is:

C_nH_2n+1OH + (1.5n)O₂ (n)CO₂ + (n+1)H₂O

Since the same two products are produced regardless of the reactant alcohol, what happens if we express the combustion enthalpy per mole of water produced, rather than per mole of alcohol consumed? Essentially, we do this by dividing by n, the number of carbons in the alcohol. (Actually we would divide by n+1, but for large molecules it effectively won't matter.) These values are also provided in the table above and are plotted below.


(Note, the figure actually shows enthalpies divided by n+1, not n. Sorry for the sloppiness.)

You can immediately see that the plot of combustion energy per mole of alcohol versus the # of carbons in the alcohol is very linear. Extrapolated to an infinitely long alcohol, the combustion enthalpy would be infinitely large! This really signifies that expressing the combustion enthalpy in this way doesn't tell you much about combustion chemistry. However, when we express the values as per carbon) produced, you can see that, with the exception of the first few alcohols, the combustion enthalpy is practically constant, no matter how many carbons are in the alcohol. It is also equal to the slope of the plot of combustion enthalpy as a function of n. In other words, the amount of energy produced per mole of water/per carbon is practically always the same, especially as n large.

If we think about the combustion processes in terms of heats of formation, we can understand why this is the case. Combusting an alcohol of n carbon atoms requires breaking n-1 C-C single bonds, 1 C-O bond, 2n+1 C-H bonds, and 1 O-H bond. As n becomes large, almost all the bond breaking is dominated by C-C and C-H bond types, and, such that, when expressed per carbon atom, you are breaking on average one C-C bond and C-H bond. Assuming that the C-C and C-H bonds always have almost the same amount of energy no matter what the molecular structure is, you should start to see why, when normalized for the amount of carbons in the alcohol chain, the combustion enthalpy never changes. (For small alcohols, the C-O and O-H bond breakings become important in the calculation, which is why methanol and ethanol are slightly different... but not much!). Note that the combustion energy for octane, a pure hydrocarbon, is -5430 kJ/mol... which when divided by the number of carbons gives a value of -678.75 kJ/mol (of carbon). Not so different from the alcohol values. When expressed this way, all molecules that are made of primarily C-C and C-H single bonds will give around the same value, reflecting that C-C and C-H single bond energies are within an approximation almost always the same energy.

Using this information, I imagine you should be able to anticipate that your second prediction is wrong. You predict that more highly branched alcohols have lower combustion enthalpies than more linear alcohols. In most cases this is not borne out by the data. Below are tables of data for the C4 and C5 branched alcohols (and ethers, for fun), presented identically as above.

Combustion data for C-4 alcohols and ethers

Alcohol		Identity		ΔHc		ΔHc per carbon atom
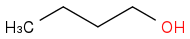		Alcohol		-2670		-668
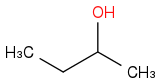		Alcohol		-2661		-665
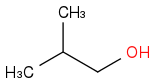		Alcohol		-2668		-667
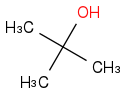		Alcohol		-2644		-665
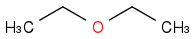		Ether		-2732		-683
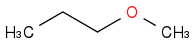		Ether		-2737		-684

Combustion data for C-5 alcohols and ethers

Alcohol		Identity		ΔHc		ΔHc per carbon
		Alcohol		-3327		-665
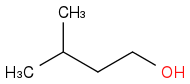		Alcohol		-3326		-665
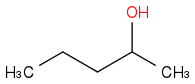		Alcohol		-3315		-663
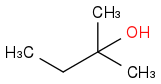		Alcohol		-3303		-661
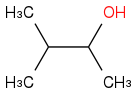		Alcohol		-3315		-663
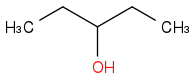		Alcohol		-3312		-662
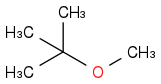		Ether		-3369		-674
		Ether		-3392		-678
		Ether		-3378		-676

Here we see several things.

First, branching doesn't make much of a difference, because branching doesn't change the relative number of C-C and C-H bonds that are being broken (in a heat-of-formation consideration). This also supports the notion that in hydrocarbons and similar molecules, all C-C and C-H bonds have the same bond enthalpies, at least to a first approximation.

Second, branched C-5 and C-4 alcohols are all virtually the same, when expressed as on a "per carbon" basis.

Third, the values of the ethers are slightly different than the values for the alcohols, reflecting the fact that an extra C-O bond is being broken instead of a C-H bond. Note that the difference between the alcohols and ethers is smaller for the C-5 molecules than the C-4 molecules. This again has to do with the fact that as the molecule grows, the C-C and C-H bonds will swamp out the average combustion enthalpy per carbon.

Just to be clear, in molecules that feature other types of bonds (double bonds, say) or unusual geometries (highly strained molecules like cubane), the combustion enthalpy will change substantially, reflecting these structural modifications. But all of this data shows that for unstrained molecules that are primarily saturated hydrocarbon in nature, it doesn't particularly matter what the structure is when it comes to properly normalized combustion enthalpy - at least once you get larger than a few carbons. Of course, from a practical standpoint, there are other considerations (density, phase, and so forth) that impact utility of a substance as a fuel.

*Except when it does.

[Lachln]

Just to be clear, intermolecular forces do not alter the standard heat of combustion? If that is so, why do isomers have different standard heat of combustion values?

Thank-you for your answer. It has helped me infinitely!

[Corribus]

Just to be clear, intermolecular forces do not alter the standard heat of combustion?

Not really, because efficient, complete combustion happens in the gas phase, even for a liquid fuel. Consider - even though your car uses liquid gasoline, it is vaporized before being combusted in the engine. This occurs in most internal combustion engines by forcing the liquid fuel through a nozzle at high pressures, a process called atomization or (in other applications) nebulization. (The same basic principle is used in a pharmaceutical inhaler.) In the vapor state, intermolecular forces are pretty much negligible. Although a liquid fuel will burn, it is primarily the vapors above the liquid that do so. This is because oxygen is an important reactant in the combustion reaction.

If that is so, why do isomers have different standard heat of combustion values?

They don't have different combustion enthalpies, at least to a good approximation, as I showed above.

[Lachln]

They don't have different combustion enthalpies, at least to a good approximation, as I showed above.


C4H10O
1-butanol: 36.05kJ/g
2-methyl-2-propanol: 32.53kJ/g

It seems to be fairly different. I don't understand?

[Lachln]

They don't have different combustion enthalpies, at least to a good approximation, as I showed above.


C4H10O
1-butanol: 36.05kJ/g
2-methyl-2-propanol: 32.53kJ/g

It seems to be fairly different. I don't understand?

Wait.. 2-methyl-2-propanol is solid at room temperature and these literature results have come from standard ambient room temperature of 21 degrees Celsius. I get it!

I can't thank you enough! Wow.

[Corribus]

One more thing:

I spent a little more time looking at the numbers for the geometric isomers above and I can kind of convince myself that the combustion enthalpies are a little less exothermic when there are branches immediately adjacent to the hydroxyl group. It's possible it's just noise, but it's a little too consistent to be chalked up as random variation IMO. For example, in the n = 4 series, butan-1-ol and 2-methyl-propan-1-ol have a combustion enthalpies of -2670 kJ/mol and -2668 kJ/mol, respectively, and these have no branches next to the hydroxyl group. 1-methylpropan-1-ol and t-butanol, which have 1 and 2 branches next to the OH group, respectively, have combustion enthalpies of -2661 and -2644 kJ/mol respectively*: the more branches next to the OH, the less exothermic the combustion. This effect is conserved in the n = 5 series. The two compounds with no branches next to the hydroxyl have combustion enthalpies of -3327 and -3326 kJ/mol, respectively; the two compounds with a single branch next to the OH have rxn enthalpies of -3315, -3315, and -3312** kJ/mol, and the compound with two branches next to the OH (1,1-dimethylpropan-1-ol) has a rxn enthalpy of -3303 kJ/mol. Similar trends for the ethers, but I won't go through and point them out.

So, to a first approximation it's true that branching doesn't affect the combustion enthalpy, but there is still some subtle effect going on that makes combustion of alcohols slightly less exothermic when they are branched adjacent to the OH.

EDIT: I had an explanation for these observations written here. I read this explanation about 5 times, and each time I liked it less, so I'm removing it for the time being. If I change my mind later, I'll post it again below.... but I will still leave my closing remark:

Man, I love chemistry.

*Just a note: the reaction enthalpy per carbon for this compound is -661 kJ/mol, not -665 kJ/mol as indicated in the table. Typo.

** And the ethyl branched compound is the least exothermic of these.